TURUNAN FUNGSI ALJABAR

A. Turunan Fungsi Aljabar Dan Rumusan Turunan

Pengertian Turunan Fungsi Aljabar

Turunan fungsi atau juga bisa disebut dengan diferensial adalah fungsi lain dari suatu fungsi sebelumnya, contohnya fungsi f dijadikan f' yang mempunyai nilai tidak memakai aturan dan hasil dari fungsi akan berubah sesuai dengan variabel yang dimasukan, atau secara umum suatu besaran yang berubah seiring perubahan besaran lainnya. Proses dalam menemukan turunan disebut sebagai diferensiasi. Lalu untuk pengertian turunan aljabar adalah perluasan dari materi limit fungsi.

Notasi turunan fungsi aljabar seperti berikut:

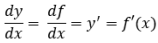
Seperti yang telah disebutkan di atas, jika turunan fungsi aljabar merupakan perluasan dari materi limit fungsi sehingga dapat didefinisikan seperti berikut:

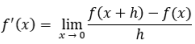
Rumus Turunan Aljabar

Setelah memahami tentang pengertian dari turunan fungsi aljabar, hal yang perlu Sobat Pintar pelajari adalah rumus dari turunan fungsi aljabar. Rumus turunan fungsi aljabar ini terbagi menjadi beberapa rumus berikut:

Turunan Fungsi Pangkat

Turunan Hasil Kali Fungsi

Bentuk dari fungsi kali adalah f(x) = u(x) . v(x), sehingga turunannya adalah f’(x) = u’(x)v(x) + u(x)v’(x).

Contoh Soal:

Turunan Fungsi Pembagian

Contoh Soal:

Turunan Pangkat dari Fungsi

Contoh Soal:

Turunan Trigonometri

B.Persamaan Garis Singgung Kurva Yg Menggunakan Turunan

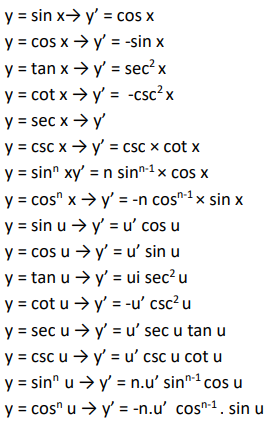
Ada beberapa cara untuk menentukan persamaan garis singgung. Mungkin ada yang memakai diskriminan atau rumus-rumus tertentu. Pada kesempatan kali ini saya akan membahas persamaan garis singgung dengan memakai turunan.

Ilustrasi untuk persamaan garis singgung pada kurva y = f(x) bisa digambarkan sebagai berikut

 

Nilai x1 = absis sedangkan y1 adalah ordinat. Hubungan antara absis dengan ordinat bisa dinyatakan dengan persamaan kurva, yaitu

y1 = f(x1)

Kemiringan garis (gradien =m) bisa dinyatakan dengan turunan y=f(x) di x1

m = f ‘(x1)

Selanjutnya persamaan garis singgung dengan gradien m dan melalui (x1, y1) bisa dinyatakan dengan

y — y1 = m(x — x1)

Contoh soal 1

Tentukan persamaan garis singgung pada kurva y = x4 — 3x3+ 6x + 7 di titik yang berabsis 2

Jawab :

x = 2
y = x4 — 3x3 + 6x + 7
y = 24 — 3.23 + 6.2 + 7 = 16 — 24 + 12 + 7 = 11
m = y’ = 4x3 — 9x2 + 6 = 4.23 — 9.22 + 6 = 32 — 36 + 6 = 2

y — y1 = m(x — x1)
y — 11 = 2 (x — 2)
y — 11 = 2x — 4
y = 2x + 7

Daftar Pustaka

https://akupintar.id/info-pintar/-/blogs/turunan-fungsi-aljabar-pengertian-rumus-aplikasi-contoh-soal

https://supermatematika.com/persamaan-garis-singgung-dengan-turunan