LIMIT
Pengertian Limit Fungsi
Limit itu suatu batas yang menggunakan konsep pendekatan fungsi. Jadi, bisa dibilang limit adalah nilai yang didekati fungsi saat suatu titik mendekati nilai tertentu. Oke, dari kasus di atas tadi, kan ada bilangan yang mendekati 2 dari kiri dan kanan. Makanya, limit itu terdiri dari limit kiri dan limit kanan. Penulisannya juga beda loh, jadi (dibaca: x mendekati 2 dari kiri) dan untuk
(dibaca: x mendekati 2 dari kiri) dan untuk  (bilangan yang mendekati 2 dari kanan
(bilangan yang mendekati 2 dari kanan
Cara Menghitung Nilai X Mendekati Satu Titik
1. Strategi Substitusi
Tahapan pertama untuk menyelesaikan suatu limit di satu titik (nilai berhingga) adalah substitusi langsung. Jika dari hasil substitusi langsung tidak diperoleh nilai dengan bentuk tak tentu seperti di bawah ini, maka nilai tersebut adalah menunjukan nilai dari limit yang bersangkutan.
Contoh soal:
2. Strategi Faktorisasi
Apabila hasil substitusi langsung diperoleh nilai bentuk tak tentu, maka kita harus memfaktorkannya sehingga bentuknya menjadi bukan bentuk tak tentu, kemudian kita lanjutkan menggunakan strategi substitusi langsung sehingga diperoleh hasilnya.
Contoh soal:
3. Strategi Mengalikan dengan Bentuk Sekawan
Strategi mengalikan dengan bentuk sekawan dilakukan pada limit berbentuk irasional. Hal ini dilakukan jika sebelumnya kita menggunakan strategi substitusi langsung dan strategi faktorisasi, hasil keduanya adalah bentuk tak tentu. Setelah perkalian itu disederhanakan, maka kita menggunakan strategi substitusi langsung lagi, sehingga diperoleh hasilnya.
Contoh soal:
B.Teorema Limit
Limit dalam bahasa umum bermakna batas.
Definisi dari limit ini menyatakan bahwa suatu fungsi f(x) akan mendekati nilai tertentu jika x mendekati nilai tertentu.
Pendekatan ini terbatas antara dua bilangan positif yang sangat kecil yang disebut sebagai epsilon dan delta.
Hubungan ke-2 bilangan positif kecil ini terangkum dalam definisi limit.

Limit 0/0
Bentuk 0/0 kemungkinan timbul dalam
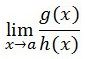
ketika kita menemukan bentuk seperti itu coba untuk sederhanakan fungsi tersebut.
Jika itu bentuk persamaan kuadrat kita bisa coba memfaktorkan atau dengan cara asosiasi, dan jangan lupa aturan a2-b2 = (a+b) (a-b).
Berikut adalah contohnya :

Limit ∞/∞
Bentuk limit ∞/∞ terjadi pada fungsi suku banyak (polinom) seperti :


Rumus cepat limit bentuk ∞/∞

- Jika m<n maka L = 0
- Jika m=n maka L = a/p
- Jika m>n maka L = ∞
Limit (∞-∞)
Bentuk (∞-∞) sering sekali muncul pada saat ujian nasional.
Bentuk soalnya sangat beragam. Namun, penyelesaiannya tidak jauh dari penyederhanaan.

Jika disubstitusikan x -> 1 maka bentuknya akan mmenjadi (∞-∞).
Dan untuk menghilangkan bentuk ∞-∞ kita sederhanakan bentuk tersebut menjadi
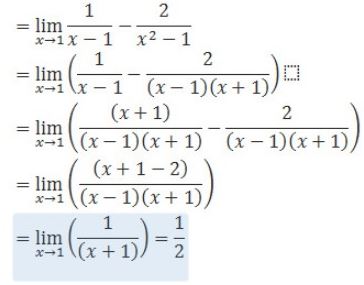
C.Rumus Cepat limit tak hingga
Rumus cepat mengerjakan limit tak hingga yang pertama dapat digunakan untuk bentuk soal limit tak hingga pada bentuk pecahan.
Untuk memperoleh nilai limit tak hingga bentuk pecahan kita hanya perlu memperhatikan pangkat tertinggi dari masing-masing pembilang dan penyebut.
Ada 3 kemungkinan yang dapat saja terjadi.
- Pertama, pangkat tertinggi pembilang lebih kecil dari pangkat tertinggi penyebut.
- Kedua, pangkat tertinggi pembilang sama dengan pangkat tertinggi penyebut.
- Ketiga, pangkat tertinggi pembilang lebih tinggi dari pangkat tertinggi penyebut.
Rumus ke-3 nilai limit tak terhingga bentuk pecahan tersebut dapat dilihat pada persamaan dibawah ini.
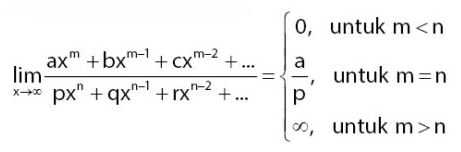

Nilai pangkat tertinggi pada pembilang adalah 3. Nilai pangkat tertinggi penyebut adalah 2 (m>n). Jadi, nilai limitnya adalah ∞.
Daftar Pustaka


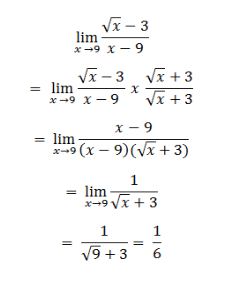
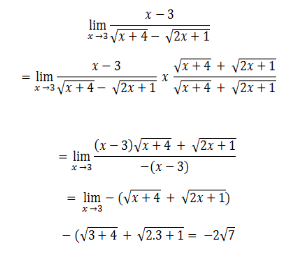
Komentar
Posting Komentar